CONTEÚDOS E METODOLOGIAS DO ENSINO DE MATEMÁTICA
Ensinar e resolver problemas é uma tarefa mais do que ensinar conceitos, habilidades e algoritmos matemáticos. Não é mecanismo direto de ensino, mas uma variedade de processos de pensamento que precisam ser cuidadosamente desenvolvidos pelo aluno com o auxilio e incentivo do professor. Um dos fatores mais difíceis de ser compreendido pelos alunos, pois exige análise, encontrar estratégias para resolução e saber executar.
Segundo Polya (1995) apud Onuchic (1999, p. 210), “resolver problemas era o tema mais importante para se fazer Matemática, e ensinar o aluno a pensar era a sua importância primeira”. Segundo o autor, para resolução de um problema devemos seguir quatro etapas. Obedecendo a ordem descrita por Polya, numere estas etapas em seguida assinale a sequência correta.
Etapa ( ) – Planejar a resolução - construir estratégias de resolução.
Etapa ( ) - Resolver o problema – colocar as estratégias em prática, resolver o problema.
Etapa ( ) Verificar a solução - ler o problema de novo e verificar se o que foi perguntado é o que foi respondido.
Etapa ( ) Compreender o enunciado – devemos ler o problema e identificar os dados fornecidos, e se possível, traçar um esquema que representa a situação.
2ª, 1ª, 4ª, 3ª.
1ª, 2ª, 4ª, 3ª.
2ª, 3ª, 4ª, 1ª.
1ª, 2ª, 3ª, 4ª.
2ª, 1ª, 3ª, 4ª.
O que é um problema?
Entende-se como problema qualquer situação em que se percebe a insuficiência dos conhecimentos imediatos diante de um desafio, exigindo uma busca de estratégias que torne possível sua solução.
Sobre o estudo acerca da resolução de problemas, assinale a alternativa errada.
Para a criança, é sempre importante criar situações pedagógicas que lhe permitam considerar os fatos fundamentais das operações, levantar hipóteses, testá-las, poder voltar atrás e refazer a trajetória.
Planejar a resolução de um problema é construir estratégias de resolução. É imaginar uma situação parecida. É analisar qual operação será desenvolvida.
A resolução de problemas não é uma atividade para ser desenvolvida em paralelo ou como aplicação de aprendizagem, mas uma orientação para a aprendizagem, pois pode proporcionar ao aluno compreender o contexto no qual se podem apreender conceitos, procedimentos e atitudes matemáticas.
O aparecimento de um problema se dá quando buscamos materiais/meios para alcançar um objetivo imediato, ocupando a maioria de nossa parte pensante com buscas incessantes para encontrar uma solução satisfatória. Devemos ler um problema e identificar os dados fornecidos, e, se possível, traçar um esquema que representa a situação.
A resolução de problemas é uma atividade para ser desenvolvida em paralelo ou como aplicação de aprendizagem, é uma orientação para a aprendizagem, pois pode proporcionar ao aluno compreender o contexto no qual se podem apreender conceitos, procedimentos e atitudes matemáticas.
Os sólidos geométricos são figuras que possuem dimensão (comprimento, altura e espessura). Eles podem ser classificados em corpos redondos (os que rolam) e poliedros (deslizam). Esses poliedros possuem elementos que são classificados como faces, arestas e vértices.
Observe o poliedro abaixo e relacione o local de cada elemento na figura.
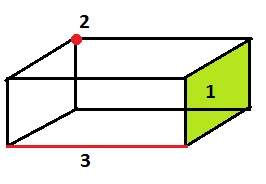
É correto apenas o que se afirma em:
Face ( 1), vértice (2), aresta (3)
Vértice ( 1), face (2), aresta (3)
Aresta ( 1), vértice (2), face (3)
Aresta ( 1), face (2), vértice (3)
Face ( 1), aresta (2), vértice (3)
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
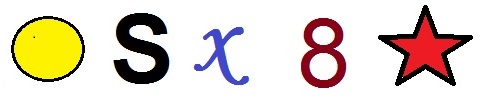
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
“Todo número natural, diferente de 1, pode ser decomposto em fatores primos, de um único modo, onde apenas a ordem dos fatores pode ser alterada”. Ou podemos dizer “todo número natural composto pode ser escrito em forma de fatores primos” RESENDE, 2006).
Por exemplo:
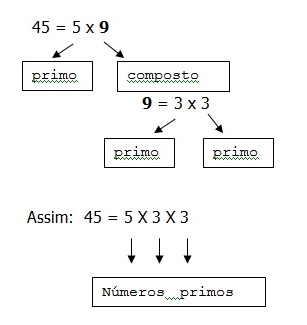
Com base nos estudos sobre decomposição de números primos, analise as alternativas abaixo, e, em seguida assinale a única alternativa errada.
28 = 2 x 2 x 7
32 = 2 x 2 x 2 x 2
220 2 x 2 x 5 x 11
180 2 x 2 x 3 x 3 x 5
120 = 2 x 2 x 2 x 3 x 5
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
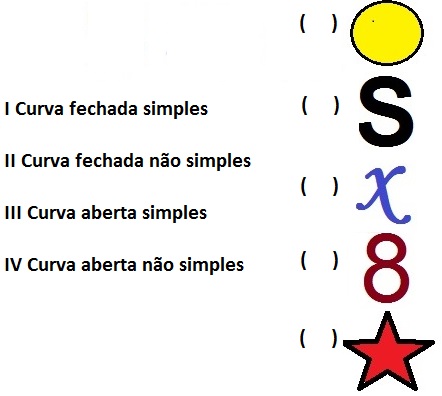
É correto apenas o que se afirma em:
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
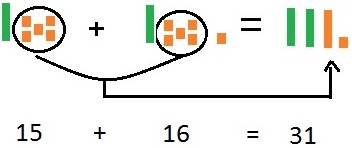
O número que está representado no Ábaco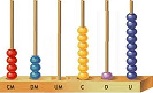 
é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
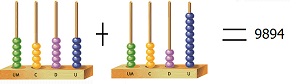
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
2ª, 1ª, 4ª, 3ª.
1ª, 2ª, 4ª, 3ª.
2ª, 3ª, 4ª, 1ª.
1ª, 2ª, 3ª, 4ª.
2ª, 1ª, 3ª, 4ª.
O que é um problema?
Entende-se como problema qualquer situação em que se percebe a insuficiência dos conhecimentos imediatos diante de um desafio, exigindo uma busca de estratégias que torne possível sua solução.
Sobre o estudo acerca da resolução de problemas, assinale a alternativa errada.
Para a criança, é sempre importante criar situações pedagógicas que lhe permitam considerar os fatos fundamentais das operações, levantar hipóteses, testá-las, poder voltar atrás e refazer a trajetória.
Planejar a resolução de um problema é construir estratégias de resolução. É imaginar uma situação parecida. É analisar qual operação será desenvolvida.
A resolução de problemas não é uma atividade para ser desenvolvida em paralelo ou como aplicação de aprendizagem, mas uma orientação para a aprendizagem, pois pode proporcionar ao aluno compreender o contexto no qual se podem apreender conceitos, procedimentos e atitudes matemáticas.
O aparecimento de um problema se dá quando buscamos materiais/meios para alcançar um objetivo imediato, ocupando a maioria de nossa parte pensante com buscas incessantes para encontrar uma solução satisfatória. Devemos ler um problema e identificar os dados fornecidos, e, se possível, traçar um esquema que representa a situação.
A resolução de problemas é uma atividade para ser desenvolvida em paralelo ou como aplicação de aprendizagem, é uma orientação para a aprendizagem, pois pode proporcionar ao aluno compreender o contexto no qual se podem apreender conceitos, procedimentos e atitudes matemáticas.
Os sólidos geométricos são figuras que possuem dimensão (comprimento, altura e espessura). Eles podem ser classificados em corpos redondos (os que rolam) e poliedros (deslizam). Esses poliedros possuem elementos que são classificados como faces, arestas e vértices.
Observe o poliedro abaixo e relacione o local de cada elemento na figura.
É correto apenas o que se afirma em:
Face ( 1), vértice (2), aresta (3)
Vértice ( 1), face (2), aresta (3)
Aresta ( 1), vértice (2), face (3)
Aresta ( 1), face (2), vértice (3)
Face ( 1), aresta (2), vértice (3)
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
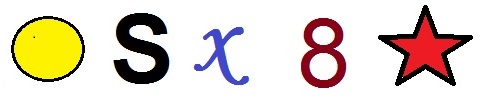
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
“Todo número natural, diferente de 1, pode ser decomposto em fatores primos, de um único modo, onde apenas a ordem dos fatores pode ser alterada”. Ou podemos dizer “todo número natural composto pode ser escrito em forma de fatores primos” RESENDE, 2006).
Por exemplo:
Com base nos estudos sobre decomposição de números primos, analise as alternativas abaixo, e, em seguida assinale a única alternativa errada.
28 = 2 x 2 x 7
32 = 2 x 2 x 2 x 2
220 2 x 2 x 5 x 11
180 2 x 2 x 3 x 3 x 5
120 = 2 x 2 x 2 x 3 x 5
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
Para a criança, é sempre importante criar situações pedagógicas que lhe permitam considerar os fatos fundamentais das operações, levantar hipóteses, testá-las, poder voltar atrás e refazer a trajetória.
Planejar a resolução de um problema é construir estratégias de resolução. É imaginar uma situação parecida. É analisar qual operação será desenvolvida.
A resolução de problemas não é uma atividade para ser desenvolvida em paralelo ou como aplicação de aprendizagem, mas uma orientação para a aprendizagem, pois pode proporcionar ao aluno compreender o contexto no qual se podem apreender conceitos, procedimentos e atitudes matemáticas.
O aparecimento de um problema se dá quando buscamos materiais/meios para alcançar um objetivo imediato, ocupando a maioria de nossa parte pensante com buscas incessantes para encontrar uma solução satisfatória. Devemos ler um problema e identificar os dados fornecidos, e, se possível, traçar um esquema que representa a situação.
A resolução de problemas é uma atividade para ser desenvolvida em paralelo ou como aplicação de aprendizagem, é uma orientação para a aprendizagem, pois pode proporcionar ao aluno compreender o contexto no qual se podem apreender conceitos, procedimentos e atitudes matemáticas.
Os sólidos geométricos são figuras que possuem dimensão (comprimento, altura e espessura). Eles podem ser classificados em corpos redondos (os que rolam) e poliedros (deslizam). Esses poliedros possuem elementos que são classificados como faces, arestas e vértices.
Observe o poliedro abaixo e relacione o local de cada elemento na figura.
É correto apenas o que se afirma em:
Face ( 1), vértice (2), aresta (3)
Vértice ( 1), face (2), aresta (3)
Aresta ( 1), vértice (2), face (3)
Aresta ( 1), face (2), vértice (3)
Face ( 1), aresta (2), vértice (3)
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
“Todo número natural, diferente de 1, pode ser decomposto em fatores primos, de um único modo, onde apenas a ordem dos fatores pode ser alterada”. Ou podemos dizer “todo número natural composto pode ser escrito em forma de fatores primos” RESENDE, 2006).
Por exemplo:
Com base nos estudos sobre decomposição de números primos, analise as alternativas abaixo, e, em seguida assinale a única alternativa errada.
28 = 2 x 2 x 7
32 = 2 x 2 x 2 x 2
220 2 x 2 x 5 x 11
180 2 x 2 x 3 x 3 x 5
120 = 2 x 2 x 2 x 3 x 5
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
Face ( 1), vértice (2), aresta (3)
Vértice ( 1), face (2), aresta (3)
Aresta ( 1), vértice (2), face (3)
Aresta ( 1), face (2), vértice (3)
Face ( 1), aresta (2), vértice (3)
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
“Todo número natural, diferente de 1, pode ser decomposto em fatores primos, de um único modo, onde apenas a ordem dos fatores pode ser alterada”. Ou podemos dizer “todo número natural composto pode ser escrito em forma de fatores primos” RESENDE, 2006).
Por exemplo:
Com base nos estudos sobre decomposição de números primos, analise as alternativas abaixo, e, em seguida assinale a única alternativa errada.
28 = 2 x 2 x 7
32 = 2 x 2 x 2 x 2
220 2 x 2 x 5 x 11
180 2 x 2 x 3 x 3 x 5
120 = 2 x 2 x 2 x 3 x 5
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
“Todo número natural, diferente de 1, pode ser decomposto em fatores primos, de um único modo, onde apenas a ordem dos fatores pode ser alterada”. Ou podemos dizer “todo número natural composto pode ser escrito em forma de fatores primos” RESENDE, 2006).
Por exemplo:
Com base nos estudos sobre decomposição de números primos, analise as alternativas abaixo, e, em seguida assinale a única alternativa errada.
28 = 2 x 2 x 7
32 = 2 x 2 x 2 x 2
220 2 x 2 x 5 x 11
180 2 x 2 x 3 x 3 x 5
120 = 2 x 2 x 2 x 3 x 5
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
28 = 2 x 2 x 7
32 = 2 x 2 x 2 x 2
220 2 x 2 x 5 x 11
180 2 x 2 x 3 x 3 x 5
120 = 2 x 2 x 2 x 3 x 5
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
É correto apenas o que se afirma em:
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
I, II, IV, III, I
I, III, IV, II, I
I, IV, III, II, I
I, II, II, IV, I
I, III, IV, I, II
‘A atividade matemática escolar não é “olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade.... Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática’.
(Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.19 ).
Com base nesta citação e nos estudos realizados sobre a compreensão do nosso sistema de numeração pela criança, percebemos que a mesma se torna muito mais fácil e com significado se utilizamos de recursos didáticos como o ÁBACO, MATEIAL DOURADO e o QUADRO VALOR DE LUGAR.
Isto posto, oriento que leia as afirmativas abaixo e assinale a única errada.
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
O número que está representado no Ábaco é: 91.734
Um dos mais antigos instrumentos de contagem é o Ábaco, podemos dizer que ele é um dos primórdios do computador. Ábaco significa quadro de contar. Os Ábacos mais antigos eram formados de sulcos feitos na areia, nos quais eram colocadas pedrinhas. Atualmente ele é formado por uma moldura de madeira com bastões paralelos, dispostos no sentido vertical ou horizontal.
O número representado abaixo no quadro valor de lugar: é: 5 143, ou seja, 3 unidades, 4 dezenas, 1 centena e 5 milhares.
Para examinarmos qual o conjunto de divisores de um determinado número, devemos considerar este número como um produto e os seus divisores serão todos os fatores deste produto.
Sobre os divisores de um número temos:
A. Apenas o número zero tem infinitos divisores.
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Analisando estas afirmativas podemos dizer que: assinale a alternativa correta.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
B. O conjunto dos divisores dos números diferentes de zero é finito.
C. O maior divisor de um número é o próprio número.
D. O número zero não e divisor de número algum.
E. Existem números que só tem dois divisores: o número 1 e ele mesmo.
Estão corretas as afirmativas A, B, C e D.
A afirmativa A está incorreta.
Estão corretas as afirmativas A, B e E.
Todas alternativas estão corretas.
Apenas a afirmativa D está incorreta.
Um número é formado de quatro algarismos, sendo o algarismo das centenas desconhecido.
8 X 7 2 = ?
Sobre os processos de divisibilidade classifique as afirmativas abaixo em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- Este número pode ser divisível por 2.
- Este número pode ser divisível por 3.
- Este número pode ser divisível por 5.
- Este número pode ser divisível por 4.
- Este número pode ser divisível por 10.
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V
A multiplicação é uma operação utilizada para simplificar a soma de parcelas iguais. No caso da multiplicação de números fracionários, deve ser realizada seguindo algumas regras básicas, como multiplicar numerador por numerador e denominador por denominador.
Com base nestas afirmativas resolva a operação e assinale a alternativa que apresenta a resposta correta.
2/3 X 3/4 = ?
F, V, V, F, V
V, V, F, V, F
V, V, V, V, V
F, V, V, V, V
V, F, F, V, V